Eng. de Software | Projeto e otimização de banco de dado | Álgebra Relacional
A álgebra relacional pode ser definida como uma linguagem de consulta formal, uma coleção de operações de alto nível sobre relações ou conjuntos. O pesquisador E. F. Codd propôs tal álgebra como a base das linguagens de consulta de banco de dados em seu modelo relacional de dados.
A principal aplicação da álgebra relacional é sustentar a fundamentação teórica de banco de dados relacional, particularmente linguagem de consulta para tais bancos de dados, entre os maiores o SQL.
Na álgebra relacional alguns operadores são primitivos e os outros são derivados em termos dos primitivos.
Linguagens Formais de Consulta ao Modelo Relacional
- Álgebra Relacional
- Linguagem procedural.
- Cálculo Relacional
- Relaciona Linguagem não procedural ou linguagem declarativa.
Álgebra relacional
Provê um fundamento formal para operações do modelo relacional.
Utilizada como base para implementar e otimizar as consultas nos sistemas gerenciadores de banco de dados relacional (SGBDRs).
Operadores da álgebra relacional
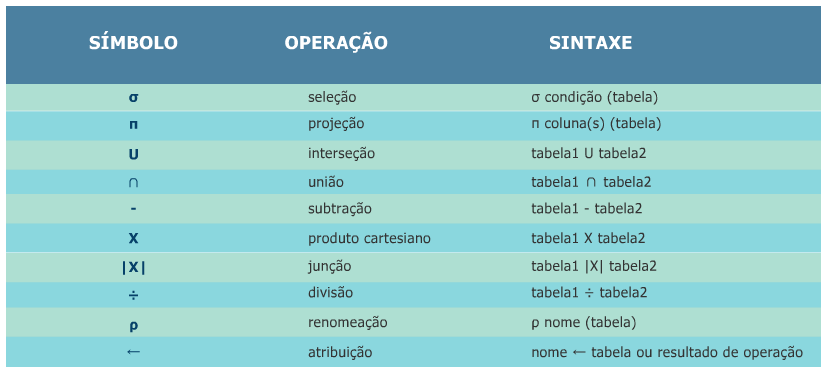
Classificações da álgebra relacional quanto à sua origem
Cinco operadores são ditos primitivos ou fundamentais, ou seja, através deles qualquer expressão de consulta de dados é possível. São eles: seleção, projeção, produto cartesiano, união e diferença.
Derivam dos operadores fundamentais. São definidos para facilitar a especificação de certos procedimentos. São eles: interseção, junção (normal e natural) e divisão.
Operadores que não se enquadram nos itens anteriores. São eles: renomeação e alteração.
Classificações da álgebra relacional quanto ao número de relações
Operam em uma única tabela. São eles: seleção, projeção, renomeação e alteração.
Operam em duas tabelas. São eles: união, interseção, diferença, produto cartesiano, junção e divisão.
Classificações da álgebra relacional quanto à área matemática
Operadores adicionais, definidos pela álgebra relacional para manipulação de dados. São eles: seleção, projeção, junção, divisão, renomeação e alteração.
Operadores usuais da teoria de conjuntos da matemática. São eles: união, interseção, diferença e produto cartesiano.
Funções matemáticas de agregação para uma coleção de valores de dados.
Entre as mais comuns estão a soma, média, máximo, mínimo e contador.
Operações primitivas da álgebra relacional
Modelo de Dados – Exemplo
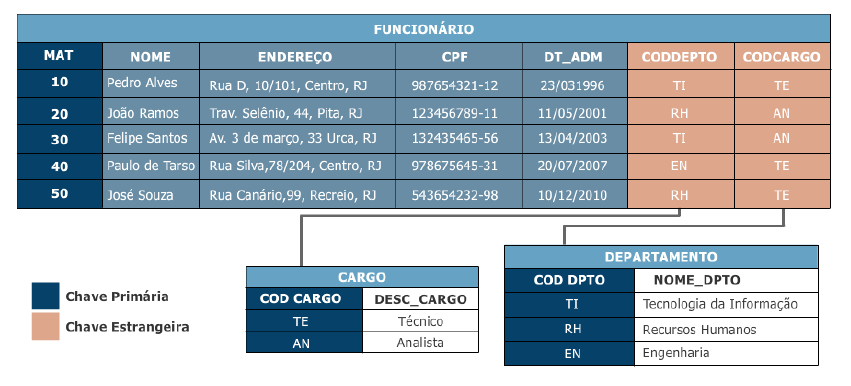
Operação de projeção
Representada pela letra grega PI, é uma operação que produz um subconjunto com os atributos passados como argumento e com todas as linhas do conjunto inicial. É classificada como uma operação unária por operar sobre apenas um conjunto de entrada.
π nome_coluna1, nome_coluna2, … , nome_colunaN (nome_tabela)
Argumentos: nome_coluna1, nome_coluna2, … , nome_colunaN
Conjunto de Entrada: nome_tabela (relação)
Exemplo 1:
Mostrar o nome de todos os funcionários.
π NOME (FUNCIONÁRIO)
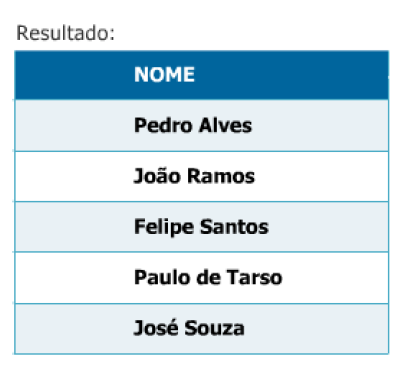
Exemplo 2:
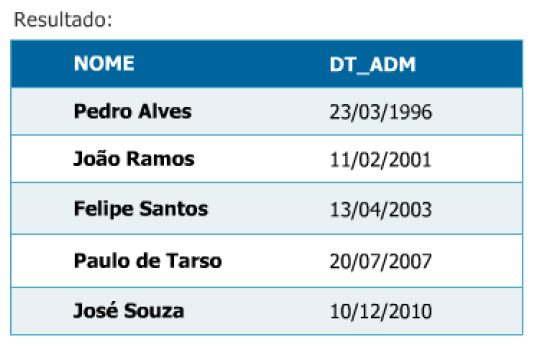
Mostrar o nome e a data de admissão de todos os funcionários.
π NOME, DT_ADM (FUNCIONÁRIO)
Operação de seleção
Representada pela letra grega sigma, é uma operação que produz um subconjunto com os mesmos atributos do conjunto inicial, porém com as linhas que satisfazem a uma determinada condição (chamada de predicado). A seleção pode ser entendida como uma operação que filtra as linhas de uma relação (tabela), e é uma operação unária, pois opera sobre um único conjunto de dados.
σ predicado (nome_tabela)
Argumentos: predicado (filtro)
Conjunto de Entrada: nome_tabela
Exemplo 1:
Selecionar os funcionários que são analistas (código do cargo ‘AN’)
σ CODCARGO=’AN’ (FUNCIONÁRIO)
Exemplo 2:
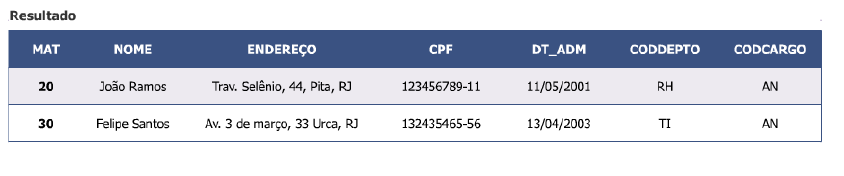
Selecionar os funcionários que são analistas (código do cargo ‘AN’) e que pertencem ao departamento de Tecnologia da Informação (código do departamento ‘TI’)
σ CODCARGO=’AN’ ^ CODDEPTO=’TI’ (FUNCIONÁRIO)

Exemplo 3:
Selecionar os funcionários que são analistas (código do cargo ‘AN’) ou que pertencem ao departamento de Recursos Humanos (código do departamento ‘RH’)
CODCARGO=’AN’ v CODDEPTO=’RH’ (FUNCIONÁRIO)

Operação de projeção com seleção
Uso combinado das operações de seleção para filtrar linhas e projeção para delimitar colunas em um subconjunto resultante.
π nome_coluna(s) (σ predicado (nome_tabela))
Exemplo 1:
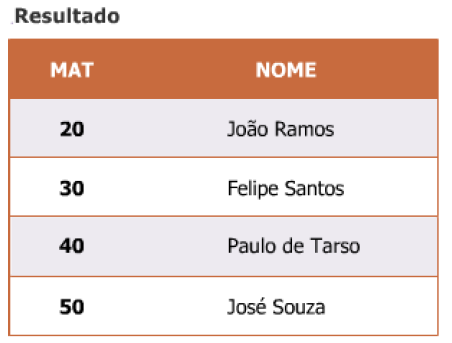
Selecionar a matrícula e o nome dos funcionários admitidos após o ano de 2001.
π MAT, NOME (σ DT_ADM ≥ ’01/01/2001’ (FUNCIONÁRIO))
Exemplo 2:
Selecionar nome e data de admissão dos funcionários admitidos após o ano de 2001 e que não são analistas (código do cargo ‘AN’).
π NOME, DT_ADM (σ DT_ADM ≥ ’01/01/2001’ ^ CODCARGO ≠ ’AN’ (FUNCIONÁRIO))

Produto Cartesiano
O produto cartesiano de duas relações ou tabelas tem como resultado uma terceira relação contendo todas as combinações possíveis entre os elementos das relações originais.
A relação ou tabela resultante terá um número de colunas que é igual à soma das quantidades de colunas das duas relações iniciais, e um número de linhas igual ao produto do número de suas linhas. Dessa forma, o produto cartesiano de uma relação 1 que possua 5 colunas e 3 linhas com uma relação 2 com 2 colunas e 5 linhas, a relação resultante terá 5+2 = 7 colunas e 3*5 = 15 linhas.
Exemplo 1:
Produto cartesiano de funcionários e cargos.
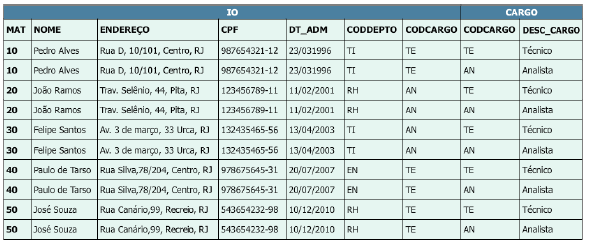
Resultado:
—– (falta) ——
Produto cartesiano com projeção e seleção
Uso combinado das operações de seleção, projeção com produto cartesiano para produzir um subconjunto resultantes com linhas e colunas filtradas e os dados de mais de uma tabela.
Exemplo 1:
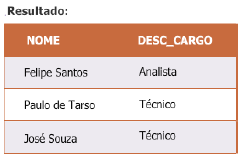
Selecionar o nome do funcionário e a descrição do seu cargo (atributo DESC_CARGO) para funcionários admitidos à partir de 2003.
π NOME, DESC_CARGO (σ DT_ADM ≥ ’01/01/2003’ ^ FUNCIONÁRIO.CODCARGO = CARGO.CODCARGO(FUNCIONÁRIO X CARGO))
União
O resultado é uma relação que contém todas as linhas da primeira relação seguidas de todas as linhas da segunda relação. A relação resultante possui a mesma quantidade de colunas que as relações originais, e tem um número de linhas que é no máximo igual à soma das linhas das relações fornecidas como operandos, já que as linhas que são comuns a ambas as relações aparecem uma única vez no resultado. As relações devem possuir o mesmo número de atributos.
Modelo de dados – exemplo
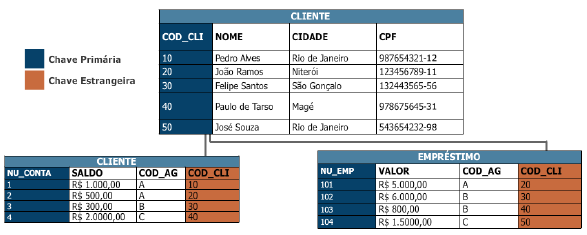
Exemplo 1:
Relacionar o nome dos clientes que têm conta ou empréstimo.
π NOME (σ CLIENTE.COD_CLI=CONTA.COD_CLI (CLIENTE X CONTA))
π NOME (σ CLIENTE.COD_CLI=EMPRESTIMO.COD_CLI (CLIENTE X EMPRÉSTIMO))
R1 = π NOME (σ CLIENTE.COD_CLI=CONTA.COD_CLI (CLIENTE X CONTA))
R2 = π NOME (σ CLIENTE.COD_CLI=EMPRESTIMO.COD_CLI (CLIENTE X EMPRESTIMO))
R3 = R1 U R2


Interseção
Produz como resultado uma relação que contém, sem repetições, todos os elementos que são comuns às duas tabelas fornecidas como operandos. As relações devem possuir o mesmo número de atributos.
Exemplo 1:
Relacionar o nome dos clientes que têm conta e empréstimo.
π NOME (σ CLIENTE.COD_CLI=CONTA.COD_CLI (CLIENTE X CONTA))
π NOME (σ CLIENTE.COD_CLI=EMPRESTIMO.COD_CLI (CLIENTE X EMPRESTIMO))
R1 = π NOME (σ CLIENTE.COD_CLI=CONTA.COD_CLI (CLIENTE X CONTA))
R2 = π NOME (σ CLIENTE.COD_CLI=EMPRESTIMO.COD_CLI (CLIENTE X EMPRESTIMO))
R3 = R1 R2

Diferença
O resultado é uma relação que possui todas as linhas que existem na primeira relação e não existem na segunda. As relações devem possuir o mesmo número de atributos.
Exemplo 1:
Relacionar o nome dos clientes que têm conta e não têm empréstimo.
π NOME (σ CLIENTE.COD_CLI=CONTA.COD_CLI (CLIENTE X CONTA))
π NOME (σ CLIENTE.COD_CLI=EMPRESTIMO.COD_CLI (CLIENTE X EMPRÉSTIMO))
Resultado:
R1 = π NOME (σ CLIENTE.COD_CLI=CONTA.COD_CLI (CLIENTE X CONTA))
R2 = π NOME (σ CLIENTE.COD_CLI=EMPRESTIMO.COD_CLI (CLIENTE X EMPRESTIMO))
R3 = R1 ∩ R2


Junção
O resultado da operação junção é uma relação com todas as combinações das tuplas na relação1 (R1) e relação2 (R2) que satisfazem a condição de junção.
Exemplo 1:
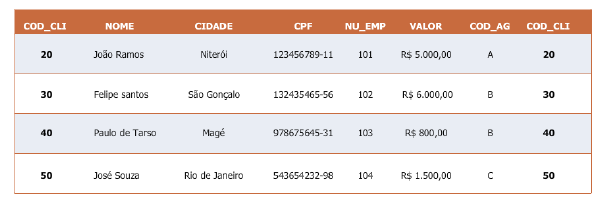
Relacionar todas as informações dos clientes que têm empréstimos.
CLIENTE |X| CLIENTE.COD_CLI=EMPRÉSTIMO.COD_CLI EMPRÉSTIMO
Resultado:
Junção natural
Quando os atributos usados na condição de junção têm o mesmo nome nas duas relações não é necessário especificá-los. Dá-se o nome de junção natural.
Exemplo 1:
Relacionar o nome e CPF dos clientes do Rio de Janeiro que têm empréstimos.
π NOME, CPF (σ CLIENTE.CIDADE=’RIO DE JANEIRO’(CLIENTE |X| EMPRESTIMO))
Obs.: A coluna COD_CLI tem o mesmo nome na tabela EMPRÉSTIMO e na tabela CLIENTE.

Atividade proposta
Atividade 1
Dadas às relações, escreva as sentenças da Álgebra Relacional que respondem às questões propostas.
a) Selecionar o código do cliente e o código da agência dos empréstimos maiores que de 300,00.
b) Selecionar os códigos dos clientes que têm conta na agência 04, mas não têm empréstimo na mesma agência.
As relações são:
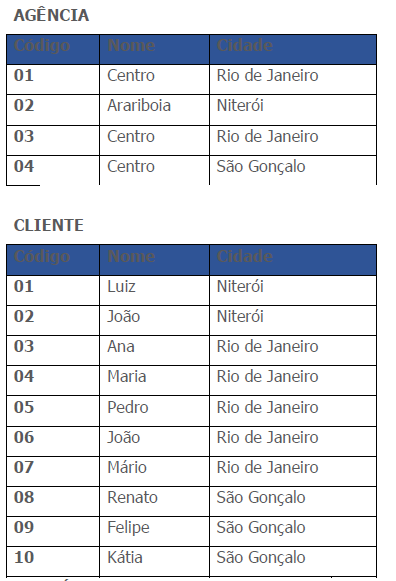
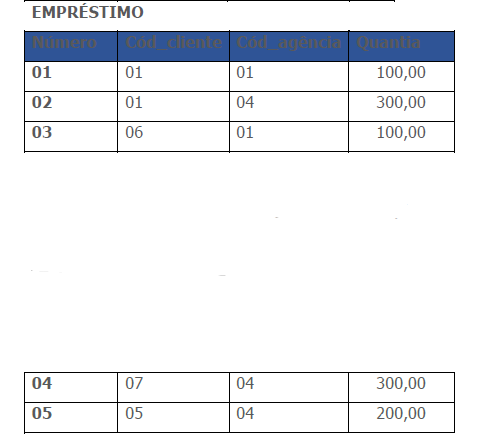
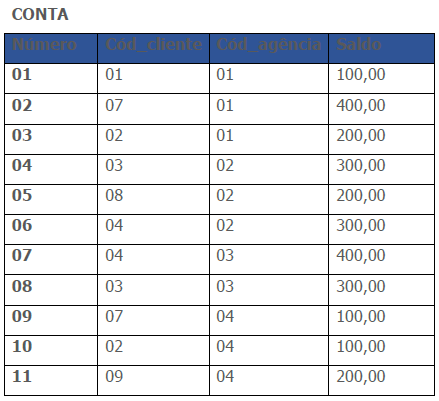
Chave de resposta:
a) π cod_cli,cod_ag (squantia > 300,00 (EMPRÉSTIMO))
b) π cod_cli (σcod_ag = 04 (CONTA) – πcod_cli (σcod_ag = 04 (EMPRESTIMO)
Referências
SILBERSCHATZ, Abraham; KORTH, Henry F; SUDARSHAN, S. A. Sistema de banco de dados. 5. ed. Rio de Janeiro: Campus, 2006.
ELMASRI, R.; NAVATHE, S. Sistemas de banco de dados. 4. ed. Pearson Education do Brasil, 2005.
Eng. de Software | Projeto e otimização de banco de dado | Álgebra Relacional